Tilting the globe

We all know that the Earth is spherical (not exactly, byt close enough for my purposes here). But what world maps seem to tell us is that is more like a cylinder. Wider at the equator, though – barrel-shaped perhaps?

Why, just look at the map:

We know that the left and right edges are really the same place; there is only one Pacific Ocean. It's not too unusual either to have seen maps where the edge is some meridian other than 180° E/W, such as this:

So we're familiar with the fact that if we keep moving east or west long enough, eventually we'll end back where we started. This striking enough that circumnavigating the globe is considered something in and of itself (Phileas Fogg never ventured south of the Equator, but is nevertheless considered to have gone around the world). But it does not feel strange, as such.

The poles, however, are weird. In the projection I have chosen here, each pole has been deformed from a point into a curve that forms the entire top or bottom edge of the map. We know, intellectually, that this is just a coordinate singularity, an artifact of the map projection. To someone actually standing on the pole, the ground will appear just as flat and featureless as it does anywhere else, modulo mountain ranges and other minor details.

But knowing is not the same as really believing. We feel vaguely – or perhaps I should stop speaking for everyone else at this point – I feel vaguely that this coordinate weirdness somehow must correspond to a real weirdness, that if I were to go there I would somehow distort along with the map, like the proverbial gedankenastronaut who falls into a black hole and finds himself stretched by infinite tides in the east-west direction.

A more everyday symptom of barrel-shaped thinking is the surprise we've all felt at some point noticing just how close to the pole a great-circle route between two distant cities goes. If you fly from London to Tokyo, the standard maps invite the assumption that you should head to the east and slightly south. But actually you should start out in a northeastern direction and pass quite close by Helsinki.

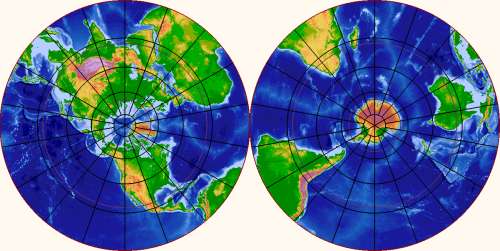
I set out to disabuse myself of the barrel-shaped fallacy. The first step is to look at a map which does not distort the poles – a pole-centered azimuthal projection:

This helps a bit, but not by much. The coordinate lines of the polar map still implicitly convey the message that the pole is a very special place. There's still a feeling that it has some momentous topological significance whether a path from point A to point B passes left or right of the the pole. Perhaps I just lack imagination, but I still find myself thinking in barrels when I look at a pole-centered map. Map globes are not much better; they tend have bearings and other special decorations at the poles which fuel the barrel fallacy directly.

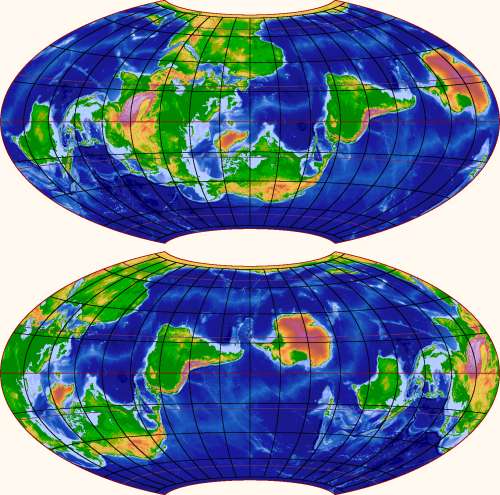
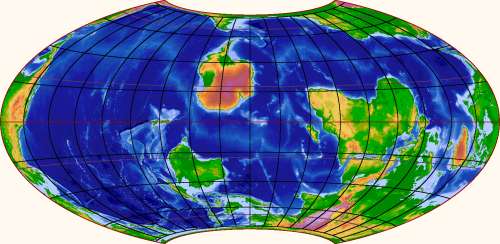
Stronger measures are needed here. The trouble seem to be the map grid – how about we draw a completely different grid over the polar regions? We could pretend that the Earth's axis passed through, say, Hawaii, and draw the world map that would result.

That sounds promising. More significantly, it sounds fun. So I wrote myself a program to draw world maps with alternative positions of the poles. I find the results convincing and fascinating. Here is the pole-at-Hawaii scenario, with two different central meridians:

The antipode to Hawaii proves to be in southern Africa, so that is where the other pole goes. The shape of Africa gets strangely distorted by the map projection, which should teach us to doubt what normal world maps tell us about the polar areas. The other continents look more recognizable, except – wonder of wonders! – the Arctic Sea is now clearly just another place.

The fascinating part comes from wondering: If the world was actually tilted to turn around the Hawaii axis (but otherwise with its current orbit and axial tilt), which climate would such a world have? Latitudes give a crude hint at the weather at different places, but that is far from the whole story. Sea currents transport large amounts of heat around the globe, and the currents would be vastly different on the tilted globe, driven as they are by winds and Coriolis forces. The winds themselves would be different; winds try to align more or less with latitudes but are deflected by mountain ranges and warped by differences in sea temperatures (which are themselves governed by currents, which are driven by winds, making the whole thing recursive). I cannot even start to answer the climate question, but I'm sure a good answer would be very interesting.

After climate comes culture. How would world history have unfolded on the tilted globe? For example, this world does not seem to need a Columbus. What, if anything, would that change? Would the Industrial Revolution still happen in a tropical, upside-down Britain? I suspect there's some pretty cool alternative-history fiction waiting to be written here.

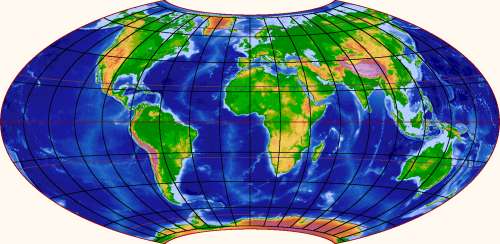
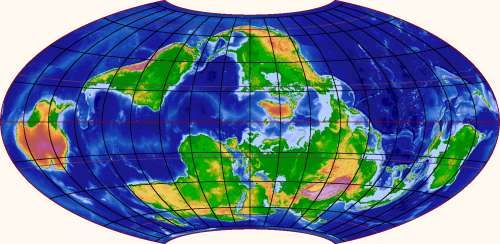
There's no reason to stop at Hawaii, of course. After creating my program, I have (mis)spent several nights looking around for interesting places to put the poles. Here is one that shows all of the continents are connected:

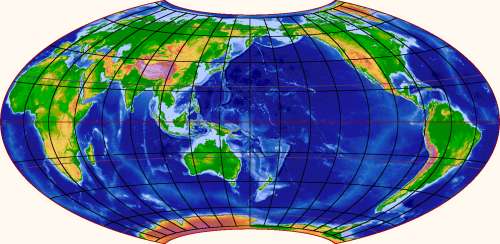
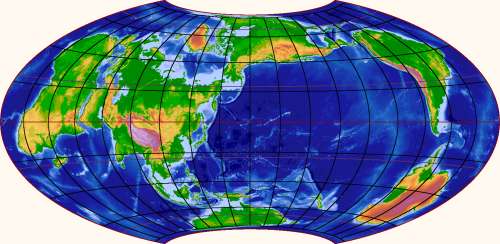
This map has the nice feature that no continental land or shelf is bisected by the edge. That is not not trivial to achieve because the edge of a world map of a somewhat orthodox shape must represent half a great circle, and there isn't much wiggle room to place it without hitting land. I think there are only three essentially different solutions; here is a second one, showing continents in a circle around the Pacific Ocean:

On the other hand, getting both poles to be covered with land is even harder. The best possibility seems to be this, which just barely does the trick:

Note here in particular that the only "wet" passage through the edge of the map is the Bering Strait (save for the wiggliness of the Panama isthmus, which the straight edge cannot quite follow). This map tries to tell you that all of the oceans are really just a single sea surrounded by land. The previous two ones try to tell you that the continents are really just a group of islands on a water planet. Both, however, show the same planet. We shouldn't believe any single map too much.

P.S. I got the shapes of continents, with elevations and sea depths as a bonus, from the ETOPO2v2 dataset, which is a marvelous resource. My only regret is that I can't drain away the icecaps of Antarctica and Greenland, but it's not obvious how to define the result of that. And it is free! You too can create cool alternative world maps if you know a programming language and some spherical geometry.